The following handwritten notes document my thinking about error bounds generally and the remainder estimation theorem for Infinite Series. The primary take away from this exercise is that bounding error in modern Calculus courses involves a mix of technology and classical methods. When the bound is determined, teachers often encourage students to use a calculator-determined limit, instead of classically determining the limit from means available at the time.
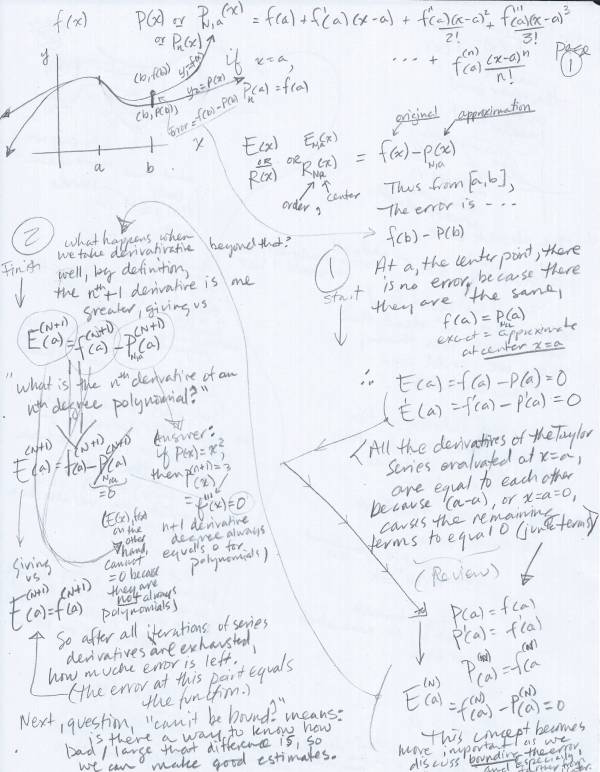
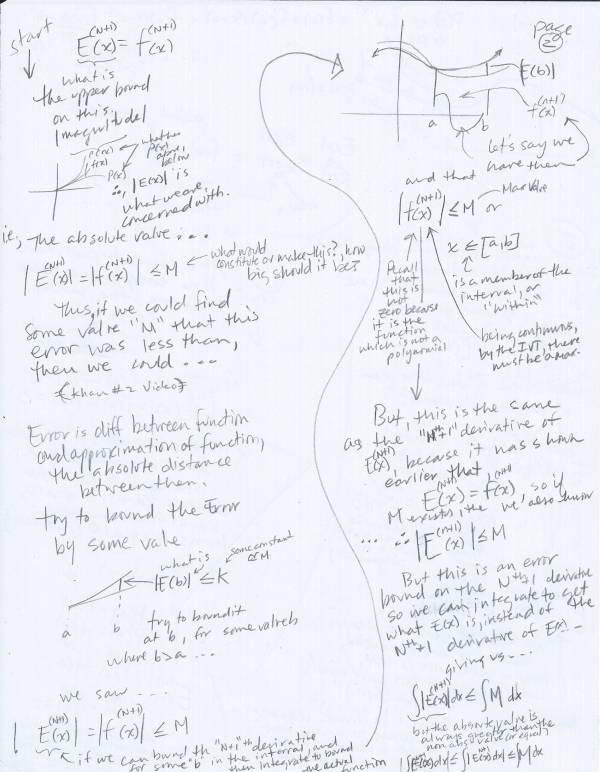



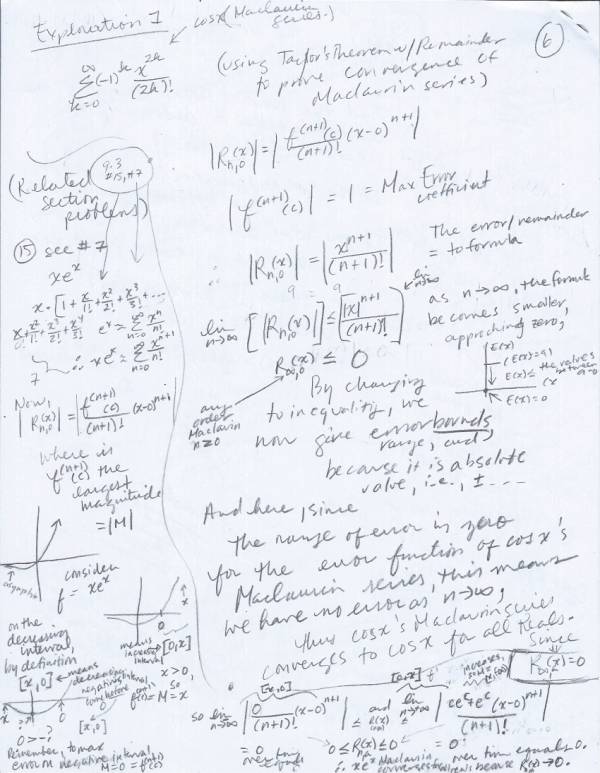
This is not a reactionary post or a post in which I argue against technology, rather, I argue that using technology this way is at odds with what the point of Infinite Series was, i.e., to approximate transcendental numbers with polynomials and arithmetic. Of course, these calculations are only done to a certain degree of precision both for the estimate itself and for the error. The question is rather why would someone use a calculator in a method that was designed to avoid using a calculator? Sure, you can do that. But is that the best approach for one’s first exploration of this topic?
Be First to Comment